面试指南之算法面试心得
本文介绍如何准备算法面试,包括算法的基础知识、面试常见问题,以及面试经验总结等,凭借本文你可以轻松拿到“offer收割机”称号。

注:本文写作于2016年,发表于小专栏,2024年整理迁移至此博客。
本文并不是要说什么高深的算法,而只是从算法面试的角度,侧重分享算法基础知识和算法面试的总结,如果把这些基础打扎实了,应付一般的开发岗位的算法面试应该是绰绰有余的。
先简单说下我的面试经历:我是在2015年参与到激烈的互联网秋招中的,当年校招头等大事就是“阿里缩招”事件,在西溪园区实习了两个月之后我很不幸地拥抱了变化。9月份回到学校之后我就开始投递简历,后来陆续拿到了腾讯、华为、美团、魅族、360、京东、爱奇艺、完美、猿题库等公司的offer。最后我选择了魅族的offer,在魅族的Flyme核心系统组工作了约半年后,我换了份工作,来到了深圳鹅厂,现在差不多快有一年鹅龄了。那年我写了篇文章“阿里宝宝漫漫求职路”,意外火爆全网,后来在朋友的建议下,我删了那篇稿子中的面试内容,只留下自己当年准备面试时写下的知识总结,感兴趣可以去看下AndroidInterviews,里面的总结加上我自己博客中的一些读书笔记基本上涵盖了大部分Android基础知识和常见面试题。非常建议你看下,也许看完了你就是“offer收割机”咯。
好了,言归正传吧,下面的内容我主要分为三部分:第一部分是算法基础知识总结,这部分的内容相对多些;第二部分是算法面试经验分享,这部分的内容是和实际算法面试有关的经验;最后一部分是附加的一些面试经验分享,希望对大家求职之路能有所帮助。
1. 算法基础知识总结
俗话说,“不积跬步,无以至千里”,要想搞定算法面试,首先要扎实算法基础。
算法基础知识总结这部分主要有以下几个内容:常见的数据结构及其实现、算法时间复杂度的计算以及常见的算法思想,其中常见的算法思想中有递归、分治、贪心、动规等等。
很显然,一篇文章是不可能将所有算法基础知识都整理出来的,下面我们主要从算法面试的角度依次谈谈这些算法基础知识,很多其他的算法例如图中的算法或者算法思想例如回溯、分支限界等都不在本文中介绍。
2014年春,我在学校里修了算法分析这门课,断断续续看了大半本《算法导论》。2014年夏,我坐在寝室里读完了《Python Algorithms》这本书。后来,我在自己的博客中写了 Python数据结构与算法设计 系列的文章,总共约十几篇,当时被微博大V Google谷歌爱好者 转发并赐新名,“码农与蛇的故事”,我挺喜欢这个名字,当然,更值得欢喜的是当时个人博客也首次迎来了那么大的访问量 😝
1.1 常见的数据结构及其实现
众所周知,数据结构是算法的基石,如果不懂二叉堆这个数据结构怎么写得出堆排序算法呢?
常见的数据结构主要有数组、链表、栈、队列、二叉堆、树、图等,其中栈和队列的题目经常出现在笔试试卷中,而且实际算法面试中二叉堆和图考得很少,经常出现的是数组、链表和二叉树这几种数据结构类型的题目。
(1) 数组虽然是最基础的数据结构,但是能考的东西却非常多,例如最常见的排序算法、找数组中第k大的数字、找两个有序数组的中位数等
[我的面试经历:美团二面遇到合并排序,友盟实习生面试二面遇到找两个有序数组的中位数]
(2) 链表因其特殊的结构也是常考点,例如反转链表、链表元素排序、合并两个有序链表、判断链表是否有环、有环的话环的起点在哪里等
[我的面试经历:腾讯实习生笔试题遇到判断链表是否有环]
(3) 二叉树由于其天然的递归结构,是最适合考查递归思想的数据结构,例如判断二叉树是否平衡、判断二叉树是否相同、判断二叉树是否对称等
[我的面试经历:神马实习生一面遇到判断二叉树是否是平衡二叉树]
(4) 栈和队列也是很重要的数据结构,但是它们往往只是作为前期的笔试题,栈经常出的题目就是给出一个栈的入栈序列,问下面哪个不可能是这个栈的出栈序列。栈和队列作为算法题并不多,常见的就是如何用两个栈来实现一个队列或者利用一个辅助栈来将一个栈中的元素排序
[我的面试经历:有道一面遇到利用一个辅助栈来将一个栈中的元素排序]
一般来说,开发岗位的算法面试是不会出题要求面试者临时设计一个数据结构来解决某个问题,大多数时候只是要求面试者能够熟练掌握常见的数据结构及其实现、能够说出这种数据结构的优缺点即可。
2015年校招时我遇到的最常问到的题是实现LRU缓存,这算是一道经典的数据结构设计题,此后的面试中再也没怎么见到过其他的数据结构设计题。
1.2 算法时间复杂度的计算
一般算法面试的时候,面试官在你给出了解法之后都会问下你这个解法的时间复杂度是多少,如果时间复杂度较高他就会要求你想出一个更优的解法,所以平时有必要练习下算法时间复杂度的计算。算法的运行时间主要有三种表示符号,但是最常见的就是大O表示法。此外,算法导论中介绍了三种时间复杂度的计算方法,分别是代换法、递归树法和主定理法。
下表是常见的算法时间复杂度值及其相应的算法问题举例,例如平方阶时间复杂度是一些基于比较的排序算法的时间复杂度,例如选择排序、冒泡排序等。nlgn阶时间复杂度是随机数字序列的最优排序算法的时间复杂度,例如快速排序等。

下表是常见的递推公式对应的算法时间复杂度和算法问题举例,例如合并排序是nlgn阶,握手问题是平方阶,汉诺塔问题是指数阶等。这个建议结合具体的例子记忆一下,以便快速反应。

下表是主定理法在三种情况下的求值公式。主定理通常可以解决类似 T(n) = a T(n/b) + f(n) 这种递归形式的问题,即将规模为n的问题划分为a个子问题,每个子问题的规模是n/b,这里a和b是正常数,划分原问题和合并结果的代价用函数f(n)描述。

1.3 常见的算法思想
(1)Induction(推导)、Recursion(递归)、Reduction(规约)和Divide and Conquer(分治)
这四个思想比较接近,在《Python Algorithms》这本书中都有提到,我放在一起介绍:
- Induction(推导)是指数学意义上的推导,类似数学归纳法,主要是用来证明某个命题是正确的。首先我们证明对于基础情况(例如在k=1时)是正确的,然后证明该命题递推下去都是正确的(一般假设当k=n-1时是正确的,然后证明当k=n时也是正确的即可)
- Recursion(递归)经常发生于一个函数调用自身的情况。递归函数说起来简单,但是实现不太容易,我们要确保对于基础情况(不递归的情况)能够正常工作,此外,对于递归情况能够将递归调用的结果组合起来得到一个有效的结果。
=> 不难发现,Induction(推导)和Recursion(递归)其实彼此相互对应,Induction是自下而上的推导(例如从n-1到n),而Recursion是自上而下的递归(例如从n到n-1)。
- Reduction(规约)是指问题转换,将一个未知的问题转换成我们能够解决的问题。
- Divide and Conquer(分治)指将原问题划分成几个小问题,然后递归地解决这些小问题,最后综合它们的解得到问题的解。
=> 仔细分析可知,Induction(推导)、Recursion(递归)和Divide and Conquer(分治)其实都是某种形式上的Reduction(规约),也就是说它们的本质都是对问题进行规约!
这四个概念有一个共同特点:它们都专注于求出目标解的某一步,我们只需要仔细思考这一步,剩下的就能够自动完成了。有点晕? 好吧,其实你可能已经对上面几个概念很熟悉了,只是平时没有这么去想过,下面我们举最常见的排序问题为例来阐述下其中的算法思想。
我们如何对排序问题进行Reduction呢?很显然,有很多种方式:
- 假如我们将原问题reduce成两个规模为原来一半的子问题,然后合并子问题的解,这是我们最为常见的二分分治策略,这样我们就得到了合并排序;
- 假如我们每次只是reduce一个元素,并假设前n-1个元素都排好序了,那么我们只需要将第n个元素插入到前面的序列即可,这样我们就得到了插入排序;
- 假如我们每次还是reduce一个元素,这次我们找到其中最大的元素然后将它让在最后一个还没有放置元素的位置上,一直这么下去我们就得到了选择排序;
- 假如我们每次还是reduce一个元素,这次我们找到第k大的元素,然后将它放在位置k上,一直这么下去我们就得到了快速排序。
怎么样?我们学过的排序算法经过这么reduce基本上都很清晰了,不是吗?
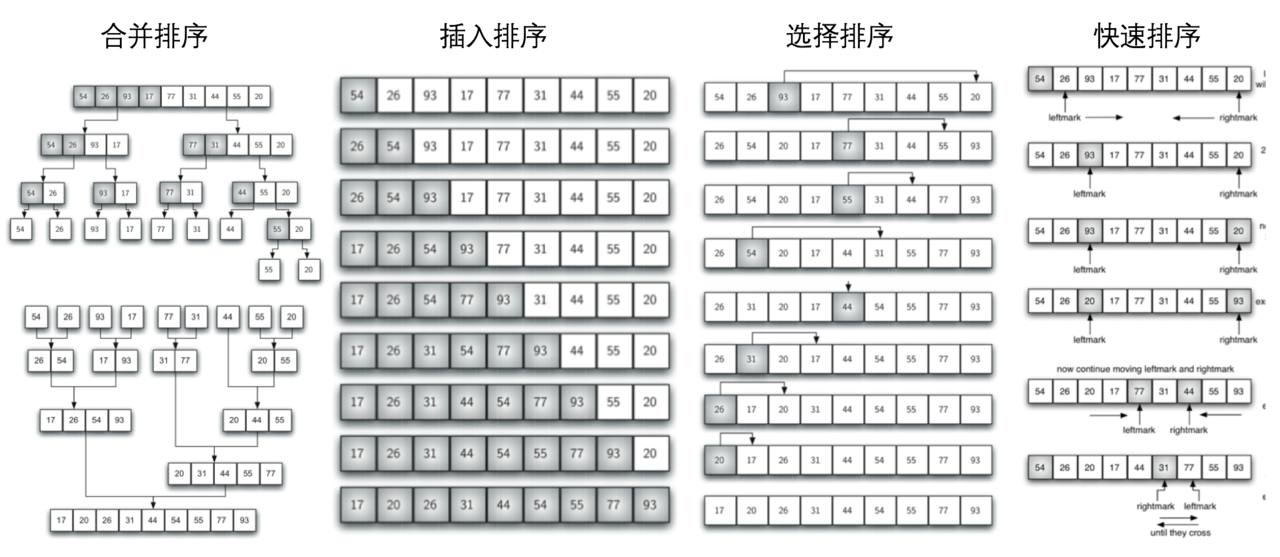
为了能够对问题使用Induction或者说Recursion,Reduction一般是将一个问题变成另一个或者几个只是规模减小了的相同问题。那么,这样做就万事大吉了吗?
其实并不是的,有些时候我们可能还需要考虑Reduction或者说分治策略的子问题平衡性。对于同一个问题,分治时采用 T(n)=T(n-1)+T(1)+n 和 T(n)=2T(n/2)+n 两种解决方案的时间复杂度是不同的,这里就不展开说了。
(2) 贪心
贪心算法顾名思义就是每次都贪心地选择当前最好的那个(局部最优解),不去考虑以后的情况,而且选择了就不能够“反悔”了。如果原问题满足贪心选择性质和最优子结构,那么最后得到的解就是最优解。
贪心算法和其他的算法比较有明显的区别,动态规划每次都是综合所有子问题的解得到当前的最优解(全局最优解),而不是贪心地选择;回溯法是尝试选择一条路,如果选择错了的话可以“反悔”,也就是回过头来重新选择其他的试试。
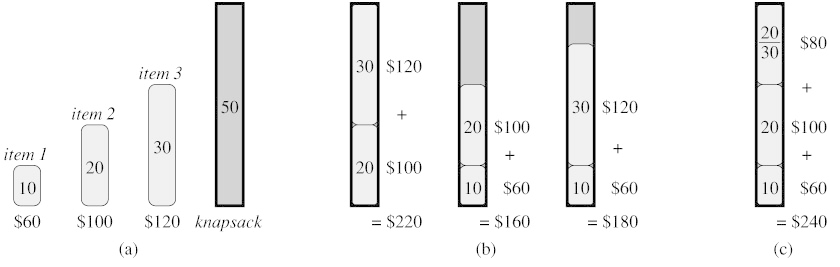
最能说明贪心算法思想的问题就是背包问题了,这个问题大家也都很熟悉了,而且该问题的变种很多,常见的有整数背包和部分背包问题。问题大致是这样的,假设现在我们要装一些物品到一个书包里,每样物品都有一定的重量w和价值v,但是呢,这个书包承重量有限,所以我们要进行决策,如何选择物品才能使得最终的价值最大呢?整数背包是说一个物品要么拿要么不拿,比如茶杯或者台灯等等,而部分背包问题是说一个物品你可以拿其中的一部分,比如一袋子苹果放不下可以只装半袋子苹果。[更加复杂的版本是说每个物品都有一定的体积,同时书包还有体积的限制等等]
很显然,部分背包问题是可以用贪心法来求解的,我们计算每个物品的单位重量的价值,然后将它们降序排序,接着开始拿物品,只要装得下全部的该类物品那么就全装进去,如果不能全部装下就装部分进去直到书包载重量满了为止,这种策略肯定是正确的。
但是,整数背包问题就不能用贪心策略了。整数背包问题还可以分成两种:一种是每类物品数量都是有限的(bounded),比如只有3个茶杯和2个台灯;还有一种是数量无限的(unbounded),也就是你想要多少有多少,这两种都不能使用贪心策略。0-1背包问题是典型的第一种整数背包问题,看下算法导论上的这个例子就明白了,在(b)中,虽然物品1单位重量的价值最大,但是任何包含物品1的选择都没有超过选择物品2和物品3得到的最优解220;而(c)中能达到最大的价值是240。
贪心算法其实还是比较好想到的,它真正难的是如何证明这个贪心策略是正确的,还有贪心算法的内在原理“拟阵”,我已忘得一干二净了。建议刷下LeetCode上的贪心题,虽然实际算法面试中很少出贪心题。
(3) 动规
动态规划其实就是一个连续决策的过程,每次决策我们可能有多种选择(0-1背包问题中我们只有两个选择,也就是对于这个物品是拿还是不拿),我们每次选择最好的那个作为我们的决策。所以,动态规划的时间复杂度其实和这两者有关,也就是子问题的个数以及子问题的选择个数,一般情况下动态规划算法的时间复杂度就是两者的乘积。
动态规划有两种实现方式:
- 一种是带备忘录的递归形式,这种方式直接从原问题出发,遇到子问题就去求解子问题并存储子问题的解,下次遇到的时候直接取出来,问题求解的过程看起来就像是先自顶向下地展开问题,然后自下而上的进行决策;
- 另一个实现方式是迭代方式,这种方式需要考虑如何给定一个子问题的求解方式,使得后面求解规模较大的问题是需要求解的子问题都已经求解好了,它的缺点就是可能有些子问题不要算但是它还是算了,而递归实现方式只会计算它需要求解的子问题。
递归实现和迭代实现的重要区别在于:递归实现不需要去考虑计算顺序,只要给出问题,然后自顶向下去解就行;而迭代实现需要考虑计算顺序,并且顺序很重要,算法在运行的过程中要保证当前要计算的问题中的子问题的解已经是求解好了的。
下面我们以有向无环图的单源最短路径问题来对比动规的两中实现方式:
假设有如下图所示的图,当然,我们看到的是这个有向无环图是经过了拓扑排序之后的结果,从a到f的最短路径用灰色标明了。
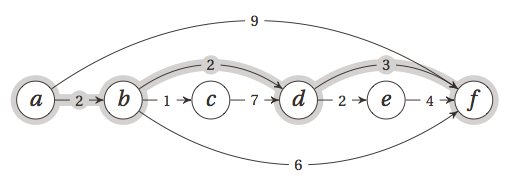
我们有两种思考方式:
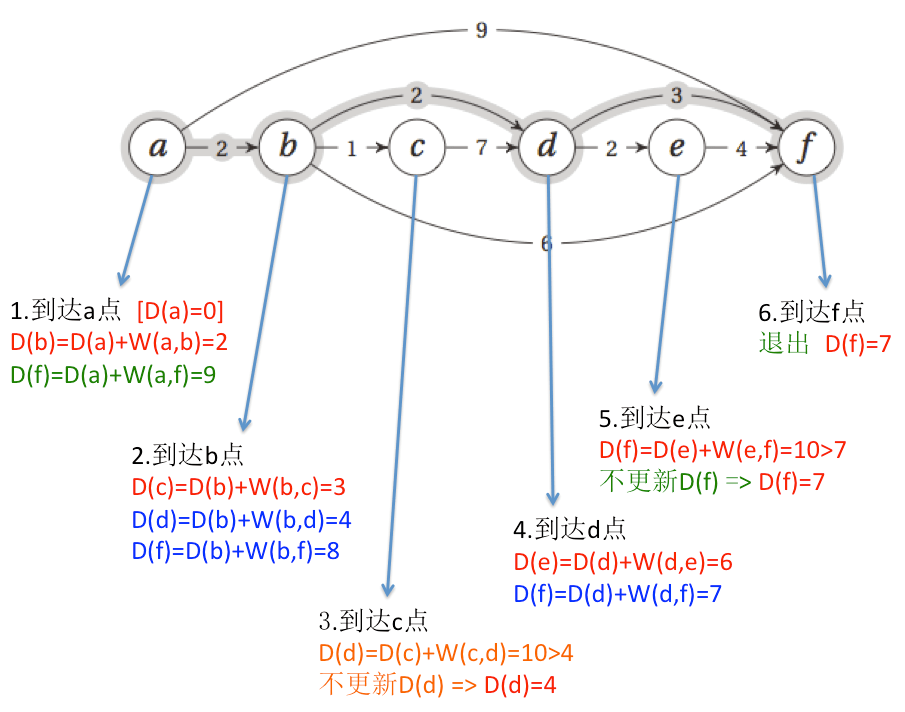
1."去哪里?":我们顺向思维,首先假设从a点出发到所有其他点的距离都是无穷大,然后,按照拓扑排序的顺序,从a点出发,接着更新a点能够到达的其他的点的距离,那么就是b点和f点,b点的距离变成2,f点的距离变成9。因为这个有向无环图是经过了拓扑排序的,所以按照拓扑顺序访问一遍所有的点(到了目标点就可以停止了)就能够得到a点到所有已访问到的点的最短距离,也就是说,当到达哪个点的时候,我们就找到了从a点到该点的最短距离,拓扑排序保证了后面的点不会指向前面的点,所以访问到后面的点时不可能再更新它前面的点的最短距离!这种思维方式的代码实现就是迭代版本。
用图来表示计算过程就是下面所示:
2."从哪里来?":我们逆向思维,目标是要到f,那从a点经过哪个点到f点会近些呢?只能是求解从a点出发能够到达的那些点哪个距离f点更近,这里a点能够到达b点和f点,f点到f点距离是0,但是a到f点的距离是9,可能不是最近的路,所以还要看b点到f点有多近,看b点到f点有多近就是求解从b点出发能够到达的那些点哪个距离f点更近,所以又绕回来了,也就是递归下去,直到我们能够回答从a点经过哪个点到f点会更近。这种思维方式的代码实现就是递归版本。
用图来表示计算过程就如下图所示:
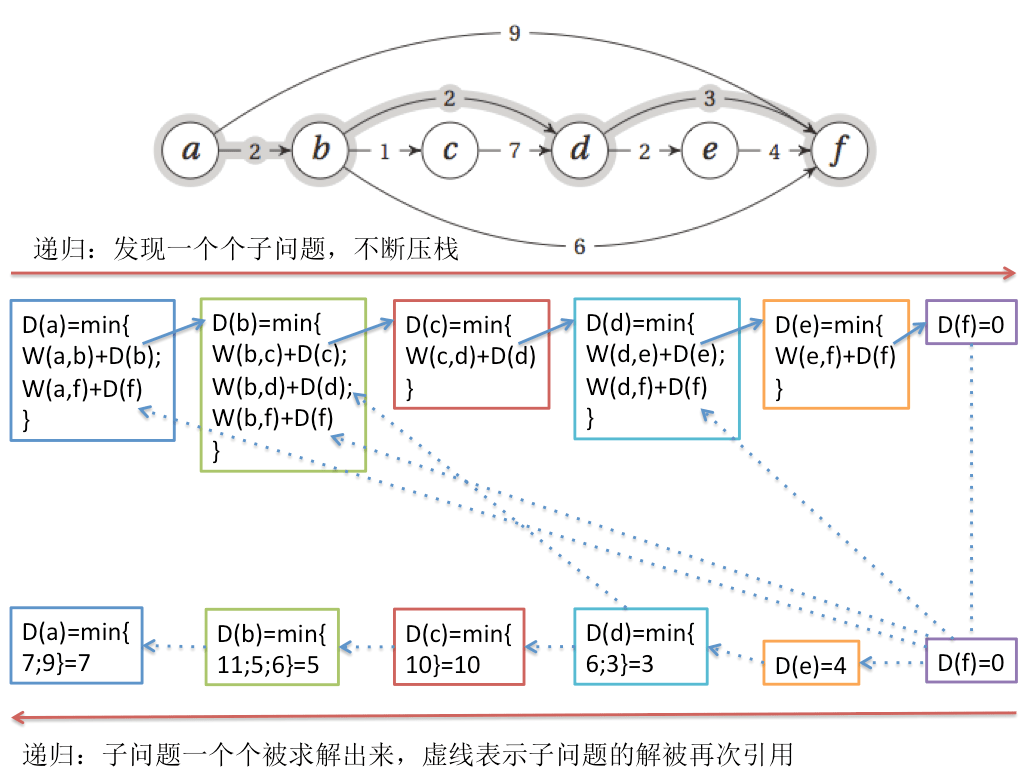
动规算法在紧张的算法面试时并不容易想出来,个人感觉就是要多练习,然后学会列出动规的递推公式,处理好边界情况,最后选择合适的实现方式去实现。实际算法面试中如果遇到水平较高的面试官是有可能出动规题的,其中最常见的就是最长公共子序列和最长递增子序列等类型的题目。
2. 算法面试经验分享
2.1 关于刷算法题
如果Github是程序员的交友社区,那么LeetCode就是程序员的王者峡谷,这里是程序员提升自己技能的竞技场。2015年我秋招的时候LeetCode也才100-200道题左右,现在竟然有近700道题啦!不论你觉得自己算法水平如何,我都建议在算法面试准备阶段刷一些LeetCode的题,毕竟熟能生巧嘛。AndroidInterviews上有两份PDF文档,分别是C++和Java版本的LeetCode题解,建议放到手机里面,以便随时翻看。国内很多互联网公司的面试官都不会自己去出题目,很多时候都是挑LeetCode上中等难度的题目来考面试者,如果你做过自然就胸有成竹了。
刷题也不是盲目地刷题,毕竟题目已经那么多了,建议先刷高频题(数组、链表、二叉树等类型题),如果时间充足再刷自己相对薄弱的环节,如果时间不充足的话那就直接看题看解答,可以反复看反复记。
2.2 关于手写代码
手写代码之前一定要先和面试官沟通好,确保你完全正确地理解了题目的意思,想好思路之后再开始写,否则噼里啪啦写了一堆没用而且还有错误的代码让面试官看了会留下不好的印象。在线编程和线下手写代码是没有代码提示的,所以平时有必要多练习手写代码,千万不要犯明显的基本语法错误,同时要注意代码风格,例如代码格式、变量命名、函数命名等,必要的时候做些防御性编程以及边界值检查等操作。
我有一次在线做题的时候没有仔细看要求的输出格式,导致有一小段代码白写了,被面试官指出来没看清楚题目,所以虽然我三道题都写出来了,但是表现却不是那么的完美 ☹️
2.3 关于面试沟通
一般算法面试出的题目都是很容易想到一个最直观的解法,只不过往往最直观的解法并不是最优的解法,但是千万别连最直观的解法都不说。例如经典的Two Sums问题,很明显,如果你列出所有两个数字的组合然后看这个组合是否满足条件也能得到问题的解,只不过你心里知道这样做的话时间复杂度太高了。但是你一定要和面试官交流的,在没有直接想出最优解的情况下你可以先说出最直观的暴力解法,利用这段时间慢慢思考有没有其他的更优的解法,或者在你说完最直观的解法之后面试官会问你有没有更好的解法,你相当于给面试官一个台阶嘛,给他次机会来引导你找到最优的解法,这样他开心你也开心不是?
这个我印象比较深刻的是那年华为的面试,面试官看起来应该是一个“久经沙场”的程序员,但是面容和蔼,是个慈祥的老先生。他第一个问题是找素数,他不停地问我“你这个解法还能不能再优化”,跟他沟通的时候你就会特别地舒服,因为老先生并不着急,他就是希望你能够在他的指引下找到更优的解法。做完这道题,我说不服,再来一道,老先生就出了第二道题,这道题感觉是他自己想出来的一道实际应用题,我在纸上圈圈画画出几个状态然后标识了状态之间如何跳转,还没画完他就拿过笔去说可以了,然后一边写一边跟我讲这个题目怎么怎么样。题目现在已经忘了,但是老先生当时给我“讲课”的神态我依稀记得,再后来我就直接去面华为专家和HR了,听说是老先生给了我很好的评价 🤓 所以,由此可见倾听与沟通是多么的重要啊!
3. 其他的面试经验分享
- 不建议去下载网上的简历模板,最好是自己亲手制作简历,表现出自己的风格,做得好给人的印象会很舒服。内容严格控制在一页,基本信息齐全,项目经历挑重点写,自己的技能树实事求是写,不要只是看过或者学过就说自己精通或者熟练。
- 适当在简历中设置一些“亮点词”,吸引面试官看到,这样他就会有兴趣对这个点进行提问,你事先想好面试官可能会问什么,然后提前准备好要回答的内容,可以的话在回答中再次设置钩子,吸引面试官继续问你,这样的话整个面试过程你就掌握了主动权。
- 对于电话面试,建议提前准备好电脑,在电脑上打开一份文档,这份文档是自己的简历以及常见问题的解答思路。一般面试官都会先让你自我介绍,这个建议提前写好,放在文档的最上面,自我介绍内容一定要精简,时间最好控制在1分钟以内。
- 如果你有自己觉得非常不错的作品的话,可以附带一份作品展示文档,多打印几份随身带在身上,或者提前安装在你的手机上,以便在面试官问到你的这个项目时,你可以直接拿出作品来,一边展示给面试官看,一边介绍你是怎么实现其中的某个界面或者功能的。
- 如果面试官问得差不多了然后问你有什么想问的,你可以考虑问经典的知乎问题,“你在xxx公司工作是怎样一种体验?”,除此之外,你可以咨询下公司的发展情况、福利待遇、加班情况等你感兴趣的内容,最好别什么都不问,别人会误以为你没有兴趣。
注:本文中部分图片来自《算法导论》和《Python Algorithms》两本书籍。


